Fractional Dynamics Research

Dr. Gary W. Bohannan, Ph.D. Montana State University (2000)

This is a multi-disciplinary project with several objectives. The ultimate goal is to develop a new definition of the calculus integral operator to better model the dynamics of evolving complex physical systems. We will be looking for systems that exhibit changes in their dynamics over relatively short time scales. Our challenge is to develop mathematical models that describe and then predict changes in the response of complex systems due to changes in the external environment. This will extend the theory of fractional calculus beyond constant order [1].

This carries on the work by Dr. Hanneken and Dr. Achar on fractional calculus and Dr. Franceschetti on ionic transport.

The human neuro-muscular system is a superb example of a complex system that is accurately described using fractional calculus [2]. There is every reason to expect that the neuro-muscular system can undergo significant changes, including changes to the fractional order describing the electrical responses, in real time as a result of biofeedback.

None of this will involve intrusive testing but will require compliance with Institutional Review Board procedures for collection of data from human subjects. We will start by making measurements of myo-muscular signals using skin sensors, looking for evidence of changes in the shape and timing of the signals that would indicate changes in the underlying dynamics. If this first exploratory phase does show that the human body can adjust the shape and timing of the neuro-muscular signal, we may then be able build simpler, but more sophisticated control of prosthetic devices. 

We will also explore other complex systems through development of new fractional order devices. Designing and fabricating new materials and devices should lead to additional insights into development of devices that can mimic the changes observed in the neuro-muscular system. 

Other systems undergoing nonlinear changes in their response are known as memristors. These have been suggested as models for neural activity, so such a study is appropriate in this context.

Goals and research questions:

• Build a more sophisticated model of complex system dynamics using fractional calculus
• Contribute to control of prosthetic devices using innovative signal processing
• Can people modify the myo-muscular signal shape and timing?
• Is there commonality among people as to how to do this?
• Construct fractance devices with various fractional orders
• Use the fractance devices in sensor and actuator circuits, including in prosthetic controllers
• Develop materials and techniques to study evolving fractional order, including nerve/muscle responses
• Develop improvements to the fractional order integral definition to include time-varying fractional order
• Apply to description of myo-muscular signals
  • How can we better understand/interpret the myo signals?
  • Test other materials and devices, such as memristors, as applications of dynamic system modeling
• Address the question of commonality of system dynamics functions
• How does randomness play a role? Can we relate fractal structure to fractional order impedance?
• Can we apply our findings to other bio-medical applications such as cancer detection?

Projects:

• Experiment with myoware sensor to see if people can use biofeedback to change the shape of the myo-muscular signal.
  • This will probably require development of sensor and display circuits and systems
  • Analyze the myo signals to see if they can be decomposed spectrally or by wavelets
• Try new recipes for making fractors
  • Construct circuits to test stability and linearity
  • Experiment with fractors in filter and other circuit applications
  • Can we construct circuits and systems that mimic the biological responses?
• Find ways to modify the fractional order of fractors
• Conduct literature search for studies of nerve-muscle signal structure and how the shape and timing changes with environment

Activities:

CRESH Summer 2017

During the summer CRESH program, we fabricated new fractors, a new type of electronic circuit element with a power-law type impedance of the form , where ω_C is the calibration frequency for measuring the impedance magnitude K. In the example of the Lithium based fractor made during the summer CRESH project, the value of K is 10.96 kΩ at 1 Hz. The value of the exponent is 0.351 for an average phase shift of approximately 32°. The phase varies by less than ± 2.5° over six decades of frequency. This characteristic leads to the devices often being referred to as "constant phase elements".

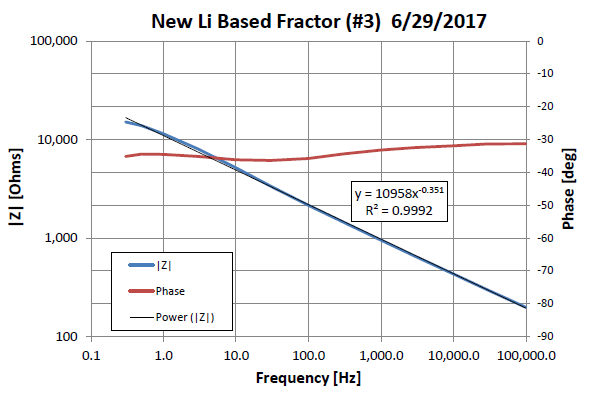
We have found that it is possible to create fractance devices with fractional orders ranging from 0.3 to 0.5. Using electronic circuits to combine multiple fractances, we have created analog fractional order operators up to 1.8 [3].

Although fractance devices have been demonstrated in physical control systems and other applications [4], general acceptance has been hampered by the lack of dynamically adjustable fractional order [5]. This is another impetus to the study of dynamically variable fractional order.

Current Activities; AY18-19

Circuit design

• Design and construction of a circuit to provide audio feedback for use in investigating various methods for providing feedback to myo-sensor participants.
• Design of optimal data collection amplifiers and filters for myo-sensor data acquisition.
• Design and testing of fractional order Van der Pol oscillator.

Biofeedback Experiment design

• Develop privacy policy and consent forms for data collection in accordance with IRB checklist.
• Develop a data collection and analysis protocol for myo-sensor feedback measurement and analysis.
• Create a procedure for consistent measurement of myo-sensor signals. 
• Compare bio-impedance measurements with surface electromyographic (sEMG) measurements.

Ionic transport background investigation

• Detailed literature search on studies of ionic transport, particularly in nerves.
• Design a bio-mimetic ionic transport cell.

Fractional Order Devices

• Fabrication of new fractors, with emphasis on obtaining a variety of fractional orders.
• Exploring use of Sodium instead of Lithium as the active ionic charge carrier.
• Exploring more efficient fabrication and assembly processes.

Collaborations:

Bio-medical applications

• Dr. Todd Freeborn, Ph.D. University of Alabama, Tuscalusa, measurements and modeling of muscular fatigue using fractional calculus. Also studying supercapacitors.
• Dr. Mark LeDoux, M.D., Ph.D., Department of Neurology & Department of Anatomy and Neurobiology, The University of Tennessee Health Science Center.

Fractional Order Devices

• Riccardo Caponetto, University of Catalonia, IT.
• Karabi Biswas, Indian Institute of Technology, Kharagpur, IN
• J. A. Tenreiro Machado, University of Porto, PT
• Antonio M. Lopes, University of Porto, PT 

Background:

There are numerous books and articles on the fractional calculus from a purely mathematical perspective. This section attempts to put the mathematics in the context of modeling physical processes. The mathematics is presented here in the context of time-domain dynamics. The fractional calculus can also be applied to spatial, long range interaction, models.

The calculus of arbitrary order was conceived as far back as the very beginnings of calculus itself, with correspondence between Leibnitz and L'Hopital concerning the interpretation of the half order derivative, d^1/2 /dx^1/2. The modern notation for the derivative is ₀D_t^q, with the integral just the anti-derivative ₀I_t^q = ₀D_t^-q, where q is the order of the operator. As implied in the notation, even derivatives are computed over a finite interval. This creates a "non-local" operator. We now know that the order of the operator can be any value, real, positive or negative, or even complex.

While there was occasional interest in the subject over the next 300 years, it was not until the 1990's that a clear understanding of how to apply the fractional order operators in physical models was developed. Ironically, it was learning how to apply cause and effect. The operators allow for non-local and long term memory effects. In particular, complex systems exhibit a wide range of time scales in their stress-strain relations, known as constitutive equations. These broad distributions of time scales are due to long range interactions that lead to power-law responses to external stimuli rather than exponential. The underlying "rule" that makes this last statement universal is the Generalized Law of Large Numbers, basically the generalization of the theory that leads to the Normal, or Gaussian, distribution but dropping the assumption of independence of the individual contributions to the sum. 

The main idea is that the history of stresses on an object plays a vital role in how the object reacts in the present. This is taken into account with the memory kernel in the fractional order integral. Memory of prior stresses is not perfect, as would be implied by the conventional integer order integral, nor is there perfect forgetting as would be implied by the linear zero-order proportional models. The strength of the memory is taken into account in the order (the exponent α) of the fractional order integral.

As the fractional calculus is generalization of the traditional integer order calculus, there are many possible forms. We will use the definitions that have been demonstrated to produce the most accurate models of physical systems under the condition of constant order. The two forms shown here can be shown to be equivalent. When the order α is unity, these reduce to the conventional first order integral. 

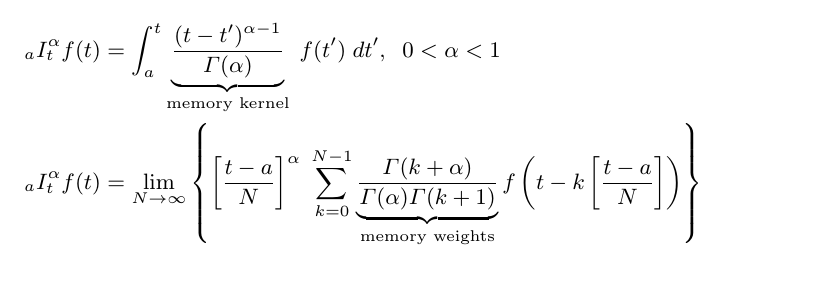
Because the operators produce results in non-integer units, these operators cannot by themselves produce physically measurable results. Other physical parameters must be included. This comment is even more appropriate when we begin to ask what happens during transients with the order changing. The operators become undefined with the dimensions of the integrand changing. There is strong evidence that the order can change over time as a result of changes in the environment. Our goal is to develop a theory of calculus that produces physically meaningful results under transient order conditions. The implication is that we may need to revise the definition of the operator to incorporate physical parameters.

Our initial model is based on electrical impedance spectroscopy, where we look at the relation between voltage measured by the myo-sensors and the the ionic current in the nerves. We now have two fractional orders to consider. The first representing memory of the voltage measured by the myo-sensors (α) and the second the memory of ionic current in the nerves (β). These can be thought of as the externally detected field and the charge transfer along the nerve. Recent work with nonlinear devices such as memristors suggest a starting point for constructing our model [6]. Generalizing the notation to include variable order,

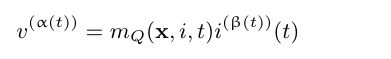 with the internal states evolving according to:

where x represents the internal states and w the external stresses.

With the notation:   , where all non-zero history must be included.  

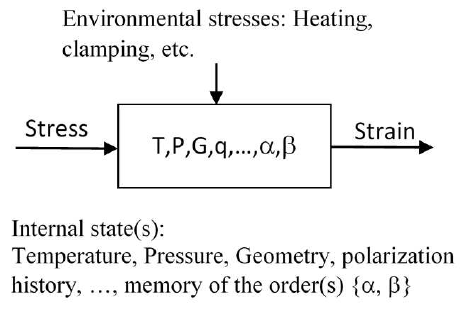
 For reference, some device models have been developed using this construct:

Our model incorporates the fractional orders as internal state functions.

We must now assume that the memory functions m_Q and the order parameters {α,β} become part of the revised evolution operator.

While this seems overwhelming at first, there has been some progress made on the analysis of fractional order differential equations. One example is the solution to the fractional harmonic oscillator [3]. A possible form of the time-varying fractional order operator is offered in [7].

References:

1. K. Oldham, J. Spanier, The Fractional Calculus; Theory and applications of differentiation and integration to arbitrary order, Academic Press, New York (1974)
2. R. L. Magin, Fractional Calculus in Bioengineering, Begell House Publishing, Connecticut (2006)
3. G. Bohannan, B. Knauber, "A physical experimental study of the fractional harmonic oscillator", in International Symposium on Circuits and Systems (ISCAS'15), 24–27 May 2015, Lisbon, 2341–2344 (2015)
4. K. Biswas, G. Bohannan, R. Caponetto, A. M. Lopes, J.A.Tenreiro Machado, Fractional-Order Devices, Springer (2017)
5. C.A. Monje, YQ Chen, B.M. Vinagre, D. Xue, V. Feliu, Fractional-order Systems: Fundamentals and Applications, Springer (2010)
6. M.-S. Abdelouahab, R. Lozi, L.O. Chua, "Memfractance: a mathematical paradigm for circuit elements with memory", Int. J. Bifurcat. Chaos 24(9), 1430023(29) (2014)
7. G. Bohannan, "Comments on time-varying fractional order", Nonlinear Dynamics, 90(3), 2137-2143, (2017)